A partir des éléments d’Euclide :
pour les visio-conférences :
- La version Powerpoint pour visio conférence
un version word95 :
- La version Word de la démonstration d’Euclide
A l’aide de démonstrations algébriques :
Ces démonstrations nécessitent l’utilisation des identités remarquables.
Première démonstration :
Cette démonstration est classique.
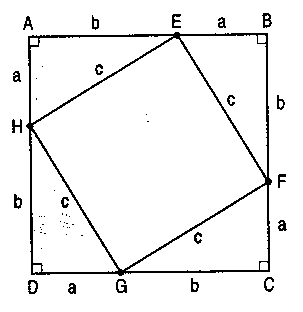1. Pourquoi le quadrilatère EFGH est-il un carré ?
2. Exprimer de deux façons différentes l’aire du grand carré et en déduire la propriété de Pythagore.
Deuxième démonstration :
Cette démonstration a été déterminée par Garfield (1831-1881), ancien président des Etats-Unis.
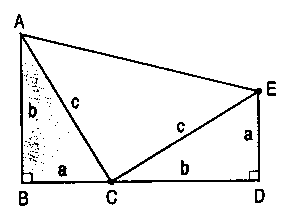
1. Expliquer pourquoi l’angle ACE est droit.
2. Exprimer de deux façons l’aire du trapèze ABDE et en déduire la propriété de Pythagore.
Troisième démonstration.
Cette démonstration a été écrite par Bhaskara (1114-1185) qui était un mathématicien hindou.
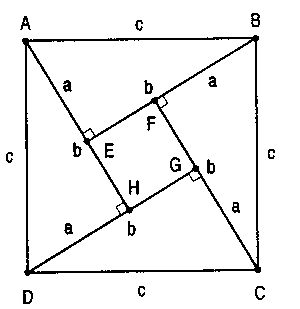
Exprimer de deux façons l’aire du grand carré et en déduire la propriété de Pythagore.
Quatrième démonstration
Dans cet exercice A désigne l’aire du triangle rectangle dont les deux côtés de l’angle droit ont pour longueur a et b.
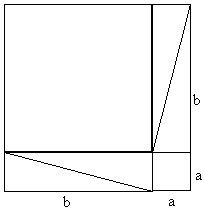
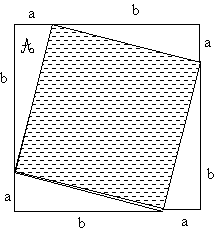
1.En justifiant la réponse, quelle est la nature du quadrilatère hachuré ?
2. Exprimer de trois manières différentes l’aire du grand carré de coté (a +b).
3. En déduire la propriété de Pythagore